ตรีโกณ

 

อัตราส่วนตรีโกณมิติ

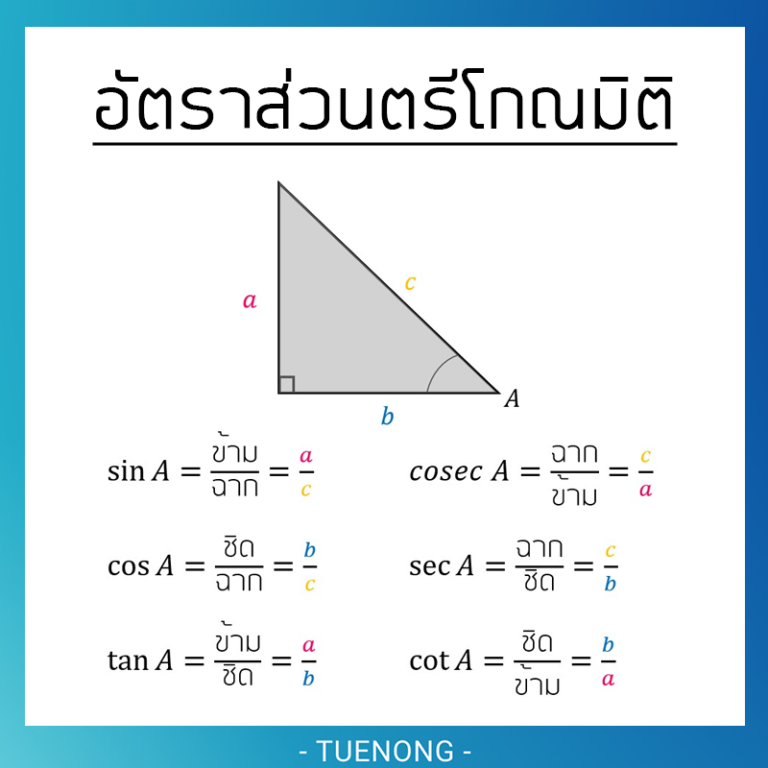
อัตราส่วนตรีโกณมิติ เป็นพื้นฐานที่สำคัญในการประยุกต์ใช้ฟังก์ชันตรีโกณมิติ ซึ่งเป็นเนื้อหาที่สำคัญและมีประโยชน์มากในทางคณิตศาสตร์ และฟิสิกส์ โดยเป็นเรื่องที่ว่าด้วยอัตราส่วนของรูปสามเหลี่ยมมุมฉาก ซึ่งมีอัตราส่วนต่าง ๆ ดังนี้

sin(A) = ข้าม / ฉาก

cos(A) = ชิด / ฉาก

tan(A) = ข้าม / ชิด

cosec(A) = ฉาก / ข้าม

sec(A) = ฉาก / ชิด

cot(A) = ชิด / ข้าม

การหาค่าตรีโกณมิติโดยใช้เทคนิค ” มือ “

การหาค่าตรีโกณมิติ โดยใช้เทคนิคมือนั้นเป็นเทคนิคที่สามารถใช้ได้ง่ายทุกสถานการณ์ โดยต้องอาศัยความเข้าใจไม่ต้องเสียเวลานั่งท่องจำมาก มาดูกันเลยว่าทำอย่างไรบ้าง

• ขั้นตอนแรก ให้เราจินตนาการตามรูป ว่านิ้วแต่ละนิ้วของเราเปรียบเสมือนค่ามุมต่าง ๆ ในตรีโกณมิติ ได้แก่ 0 , 30 , 45 , 60 และ 90 
• ถ้าต้องการหาค่าตรีโกณมิติที่มุมเท่าไหร่ให้หักนิ้วนั้นลง
• อัตราส่วนที่ได้จะเป็นดังนั้น
  • sin จะเท่ากับ สแควรูท จำนวนนิ้วที่มีด้านซ้ายมือ โดยเริ่มจากนิ้วที่หัก ส่วนด้วย 2
  • cos จะเท่ากับ สแควรูท จำนวนนิ้วที่มีด้านขวามือ โดยเริ่มจากนิ้วที่หัก ส่วนด้วย 2
  • tan จะเท่ากับ สแควรูท จำนวนนิ้วที่มีด้านซ้ายมือ ส่วนด้วยสแควรูท จำนวนนิ้วที่มีด้านขวามือ

ตัวอย่าง ถ้าเราต้องการ หาค่าตรีโกณมิติ ที่มุม 60 องศา

วิธีทำ ให้เราใช้มือขวา หักนิ้วชี้ลง จะพบว่า จะเหลือนิ้วด้านซ้าย 3 นิ้ว ( นิ้วก้อย , นาง , กลาง ) และจะเหลือนิ้วด้านซ้าย 1 นิ้ว ( นิ้วโป้ง )

เราสามารถหาค่าอัตราส่วนตรีโกณมิติได้ ดังนี้

• sin มีจำนวนนิ้วด้านซ้าย 3 นิ้ว จึงได้ค่า sin 60 = √3/2
• cos มีจำนวนนิ้วด้านขวา 1 นิ้ว จึงได้ค่า cos 60 = 1/2
• tan  มีจำนวนนิ้วด้านซ้าย 3 นิ้ว  และ มีจำนวนนิ้วด้านขวา 1 นิ้ว จึงได้ค่า tan 60 = √3/1 หรือ tan 60 = √3

ค่าตรีโกณมิติที่ควรทราบ

หัวข้อที่แล้ว เราได้เรียนรู้หาค่าอัตราส่วนตรีโกณมิติด้วยวิธีมือแล้ว คราวนี้เรามาดูตารางสรุปกันดีกว่าว่าอัตราส่วนตรีโกณมิติพื้นฐานที่เราควรทราบมีอะไรบ้าง

	0°	30°	45°	60°	90°
Sin	0	1/2	√2/2	√3/2	1
Cos	1	√3/2	√2/2	1/2	0
Tan	0	1/√3	1	√3	หาค่าไม่ได้

สมบัติต่าง ๆ ที่ควรทราบเกี่ยวกับตรีโกณมิติ

โดยจะนำมาเฉพาะที่ใช้ใน ตรีโกณ ม.3 เท่านั้น ถ้าน้อง ๆ คนไหนเรียนเกินหลักสูตรหรือต้องการเนื้อหาเพิ่มเติมสามารถไปดูบทความ ตรีโกณมิติ ตัวเต็มได้

• sin2θ + cos2θ = 1
• tan2θ + 1 = sec2θ
• cot2θ + 1 = cosec2θ
• sin(A) = 1/cosec(A)  และ cosec(A) = 1/sin(A)
• cos(A) = 1/sec(A) และ sec(A) = 1/cos(A)
• tan(A) = 1/cot(A) = sin(A)/cos(A) และ cot(A)=1/tan(A) = cos(A)/sin(A)

กฎของ SIN และ กฎของ COS

กฎของ sin และ กฎของ cos เป็นหัวข้อการประยุกต์ที่ถูกใช้เป็นประจำ ในการหาความยาวด้านและมุมของสามเหลี่ยมใด ๆ โดยใช้ความรู้ของตรีโกณมิติ แต่อย่าจำสับสน ตรีโกณมิติ อยู่บนพื้นฐานของรูปสามเหลี่ยมมุมฉาก แต่ในหัวข้อนี้นำเข้ามาประยุกต์กับสามเหลี่ยมใด ๆ เท่านั้น

กฎของ SIN

a/sinA = b/sinB = c / sinC

โดยกำหนดให้ 

a , b , c = เป็นความยาวด้านตรงข้ามมุม A , B , C ตามลำดับ

A , B , C = เป็นมุมภายในรูปสามเหลี่ยม

กฎของ COS

a2 = b2 + c2 – 2bc(cosA)

b2 = a2 + c2 – 2ac(cosB)

c2 = a2 + b2 – 2ab(cosC)

โดยกำหนดให้ 

a , b , c = เป็นความยาวด้านตรงข้ามมุม A , B , C ตามลำดับ

A , B ,C = เป็นมุมภายในรูปสามเหลี่ยม